Rear wheel inertia
After previously calculating the moment of inertia for the roller assembly, the next step was to get a more accurate figure for the rear wheel.
For this, I used the approach given at analyticcycling.com. I’d be the first to confess I don’t quite follow the maths involved, but am happy enough to trust the answer it spat out – 0.079619 kg m².
Just for the record, the complete wheel (excluding skewer) weighed in at 1669 grams on my trusty kitchen scales – and consists of a 2012 PowerTap Pro hub, 11-32 SRAM cassette, 32 hole Kinlin XR300 rim, Sapim laser spokes with alloy nipples, 23mm GP4000S clincher, a random inner tube, plus a light smattering of road grime ;)
Rotational kinetic energy
Now I have a moment of inertia for both the roller assembly and the rear wheel, it’s possible to calculate the kinetic energy of both at any given speed.
The first step is obtaining the angular velocity for both the wheel and the roller. To get this, we convert the road speed in kilometres per hour into metres per second, and from there into angular velocity (radians per second);
ω = (road speed * 0.27777777777778) * circumference * 2π
Then, from the moment of inertia and the angular velocity, can we obtain the rotational kinetic energy;
KE = ½ I ω²
Rolldown test
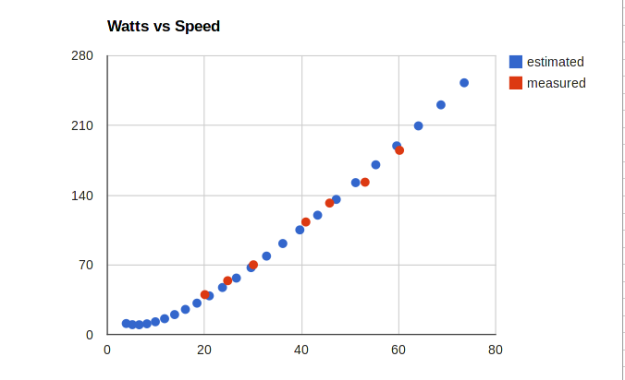
Prior to building up the speed sensor, I thought I’d perform a quick sanity check of my calculations (and my assumptions) based on some ANT+ data. So, with GC running in training mode on my laptop & collecting data via a USB ANT+ stick, I performed a number of steady speed efforts, along with couple of roll down tests.
The roll down test gives speed against time, but more usefully (thanks to the equations above) kinetic energy against time. From this data I can generate a polynomial expression for the curve, and then differentiate to get the rate of change of kinetic energy at any given speed.
That last sentence is actually the key point of this whole weighing and measuring exercise on the un-braked roller assembly. We have calculated the kinetic energy (in joules per second) that is being lost through rolling resistance at any speed, and by extension the wattage (1 watt = 1 joule per second) we would need to put back in to overcome this resistance and hold a steady state.
The final sanity check against the training mode ANT+ data consists of comparing the actual wattage required for the steady speed efforts against the expected rate of change obtained from our calculations.
At this point, I’ll call that a win! Next step is to build up the speed sensor to get some more accurate data..